Спектральный анализ колебаний в нелинейных преобразователях: метод кратных дуг, метод трех и пяти ординат, Метод функций Бесселя
Обновлено: 16.05.2024
При изучении процессов нелинейных преобразований в первую очередь приходится решать задачу нахождения спектра колебаний на выходе преобразователей. Данная задача формулируется следующим образом.
Имеется безынерционный нелинейный преобразователь, характеристика которого аппроксимируется зависимостью i = f(u). На вход этого преобразователя поступает так называемое полигармоническое колебание вида
В частном случае это может быть моногармоническое колебание вида
u(t) = Ucos(ωt + φ).
Необходимо определить спектр тока i на выходе преобразователя. Такая задача получила название «спектральный анализ». Для решения этой задачи можно использовать аппарат рассмотренных ранее рядов Фурье. Однако такой метод определения спектра отклика оказывается весьма трудоемким, поэтому на практике применяются специальные методы спектрального анализа, связанные с рассмотренными ранее методами аппроксимации характеристик нелинейных преобразователей. При этом наибольшее распространение получили:
- метод кратных дуг;
- метод формул трех и пяти ординат;
- метод функций Бесселя от мнимого аргумента;
- метод угла отсечки.
Метод кратных дуг
Данный метод является основным при использовании полиномиальной аппроксимации. Его удобно применять при анализе нелинейных преобразований в процессе модуляции, демодуляции, преобразования и деления частоты.
Пусть вольт-амперная характеристика нелинейного резистивного элемента аппроксимирована многочленом n-й степени:
На вход преобразователя подается гармоническое колебание вида
u(t) = Ucos(ωt + φ).
Выполнив соответствующие подстановки, получим
Воспользуемся следующими известными формулами:
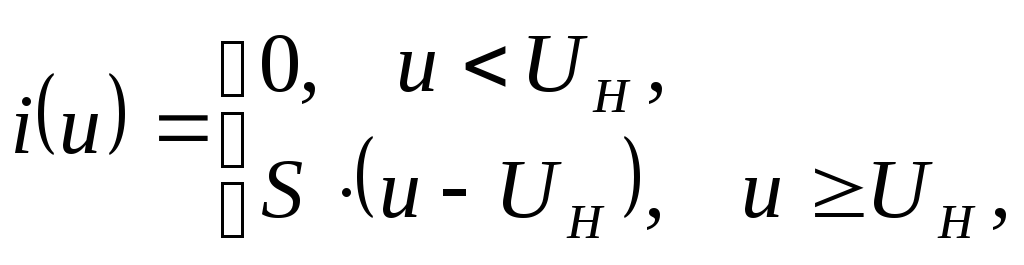
позволяющими степени косинусов (синусов) заменить тригонометрическими формулами кратных аргументов, отсюда и происходит название данного метода.
Предположим x = ωt + φ, тогда, выполнив очевидные подстановки, получим:
Здесь
При произвольном номере гармоники общее выражение для тока имеет вид
Спектр амплитуд тока на выходе нелинейного преобразователя при воздействии одного гармонического колебания показан на рис. 3.5, а.
Из сказанного можно сделать следующие выводы.
- Выходной спектр нелинейного преобразователя при воздействии гармонического сигнала является линейчатым. При этом составляющие сигнала имеют частоты, кратные частоте входного сигнала. Наивысший номер составляющей спектра равен степени аппроксимирующего полинома.
- Постоянная составляющая и амплитуды четных гармоник определяются только четными степенями напряжения.
- Значение текущей фазы k-й гармоники больше значения фазы входного сигнала в k раз, т.е. (Формула), откуда (Формула).
Ранее отмечалось, что нелинейные преобразования вызывают появление новых спектральных составляющих, которых не было на входе. Данный эффект проявляется наиболее ярко, если на вход преобразователя подается колебание, являющееся суммой нескольких гармоник с различными частотами.
Пусть на нелинейный резистивный элемент поступает так называемое бигармоническое колебание вида

Рис. 3.5. Амплитудные спектры тока на выходе нелинейною преобразователя при воздействии одного (а) и двух (б) гармонических колебаний
Для упрощения анализа рассмотрим случай, когда вольт-амперная характеристика описывается многочленом 2-й степени (т.е. слабо нелинейный режим):
Выполним соответствующие подстановки:
Из этого выражения видно, что в выходном колебании содержатся составляющие, которые имелись в спектре входного колебания, а также появились и новые гармоники. Иными словами, на выходе имеются постоянная составляющая и первые, вторые гармоники входных сигналов. Принципиально новым является появление двух комбинационных колебаний с частотами (Формула) и (Формула). Амплитуды этих колебаний, равные (Формула), в одинаковой степени зависят от амплитуд каждого из входных сигналов. Комбинационные колебания обращаются в нуль, если на входе устройства отсутствует любой из двух входных сигналов.
Спектр амплитуд тока для рассмотренного случая показан на рис. 3.5, б.
Метод трех и пяти ординат
Данный метод применяют, как правило, при графических расчетах для оценки нелинейных искажений, возникающих в модуляторах, усилителях и других устройствах. Его отличительной особенностью является то, что в нем не требуется осуществлять аппроксимацию вольт-амперной характеристики нелинейного элемента.
Метод формул трех ординат позволяет определить значения постоянной составляющей и амплитуды первых двух гармоник тока в следующем виде:
Пусть характеристика нелинейного преобразователя задана графически (рис. 3.6).

Выберем на графике три ординаты и потребуем, чтобы значения тока в этих точках совпадали с его действительными значениями. Иными словами, возьмем следующие точки:
Рис. 3.6. Определение значений гармоник тока посредством выбора ординат характеристики нелинейного преобразователя
Подставив выбранные значения в формулу для тока, получим систему из трех уравнений:
Решив эту систему уравнений относительно (Формула), получим:
Аналогично используют формулу пяти ординат для определения значений тока первых четырех гармоник. В этом случае точность расчетов будет выше. Однако в целом точность нахождения амплитуд гармоник с использованием данного метода невысока: ошибка растет с увеличением амплитуды подводимого напряжения.
Метод функций Бесселя
Данный метод применяется при анализе работы демодуляторов и преобразователей частоты в случае, когда вольт-амперная характеристика аппроксимируется экспоненциальной функцией.
Пусть имеется нелинейный преобразователь в виде полупроводникового диода, характеристика которого аппроксимирована выражением
На его вход подается напряжение
u(t) = E + Ucosωt.
Подставив это напряжение в аппроксимирующее выражение, получим
Это выражение можно представить в виде ряда Фурье, для чего необходимо найти коэффициенты разложения, использовав выражения из теории функций Бесселя:
— модифицированная функция Бесселя n-го порядка от аргумента х.
При этом x = αU, φ = ωt.
Тогда разложение в ряд Фурье будет иметь следующий вид:
Из этого разложения видно, что постоянная составляющая тока
амплитуда первой гармоники
амплитуда n-й гармоники
Расчеты по данным выражениям показывают, что с увеличением номера гармоники ее амплитуда уменьшается. При выполнении расчетов можно использовать подробные таблицы функций Бесселя, приведенные в специальных справочниках.
Метод угла отсечки
Метод угла отсечки применяют при кусочно-линейной аппроксимации вольт-амперных характеристик. Он весьма эффективен для расчетов умножителей частоты, усилителей и генераторов, собранных на полупроводниковых приборах и лампах.
Пусть имеется нелинейный преобразователь, вольт-амперная характеристика которого аппроксимирована соотношением
где S — крутизна характеристики; U0 — напряжение отсечки.
На рис. 3.7 эта характеристика представляет собой две прямые линии.
Рассмотрим воздействие напряжения
u = E + Ucosωt,
где Ε — напряжение смещения, которое определяет рабочую точку.
Из рис. 3.7 видно, что нелинейный элемент работает с отсечкой, т.е. часть входного напряжения, которая не заштрихована, не участвует в создании тока. Получаемые при этом импульсы тока характеризуются двумя величинами: высотой (Формула) и шириной, т. е. углом отсечки, который обозначен θ.
«Углом отсечки» называется часть периода колебания с частотой ω, в течение которого или ток изменяется от максимального значения до нуля, или входное напряжение изменяется от максимального U до U0. Угол отсечки θ = ωt и измеряется в градусах или в радианах. Следовательно, можно записать
откуда
Угол отсечки может принимать значения от нуля (ток не проходит) до π, что соответствует линейному режиму работы преобразователя. Если напряжение смещения Ε равно напряжению отсечки, то θ = π/2 , т. е. в этом случае проходят только положительные полупериоды входного сигнала.
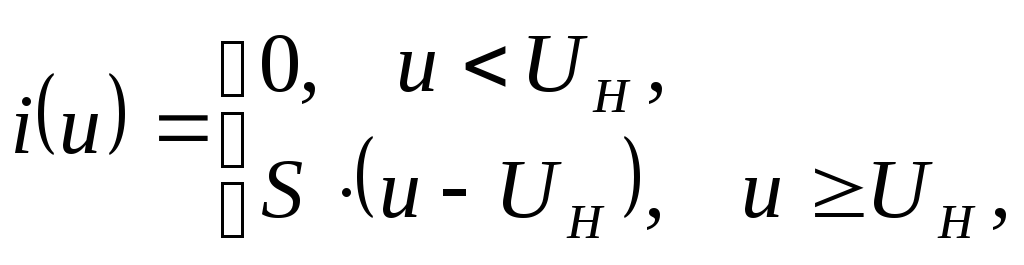
Рис. 3.7. Пояснение процессов в нелинейном преобразователе при использовании для расчета метода угла отсечки
Определим значение выходного тока. Для чего подставим выражение входного напряжения u в соотношение, которым аппроксимирована вольт-амперная характеристика:
Поскольку при ωt = θ ток равен нулю (i = 0), можно записать
Вычитанием второго выражения из первого получим
i = SU(cosωt − cosθ).
При ωt = 0 выходной ток имеет максимальное значение
, т.е.
Полученная графическим построением периодическая последовательность импульсов тока является четной функцией, поэтому ее можно представить в виде ряда Фурье, в котором содержатся постоянная составляющая и косинусоидальные гармоники:
Постоянную составляющую найдем из соотношения
— коэффициент постоянной составляющей.
Соответственно амплитуда первой гармоники
Аналогично определяется амплитуда n-й гармоники:
n = 2, 3, 4, …
Иногда при расчете удобнее использовать нормированные коэффициенты гармоник (нормированные относительно значения максимального тока (Формула)):
Эти коэффициенты являются функциями только угла отсечки θ, поэтому для них имеются справочные графики и специальные таблицы, которые удобно применять в расчетах нелинейных преобразователей. Заметим, что для наиболее часто применяемого режима при θ = π/2
Ниже, при рассмотрении различных функциональных преобразований сигналов перед нами неоднократно будет возникать задача определения спектра колебаний на выходе нелинейной цепи. Поэтому целесообразно прежде всего ознакомиться с общими методами спектрального анализа.
Задача заключается в следующем: на вход безынерционной нелинейной цепи, аппроксимируемой зависимостью
или полигармоническое колебание
Требуется определить спектр отклика, т. е. спектр тока Классический метод решения этой задачи заключается в подстановке выражений (3.4)-(3.6) в правую часть (3.3) с последующим определением спектральных компонент путем использования аппарата рядов Фурье в случае гармонического воздействия (3.4) или кратных рядов Фурье в случае бигармонического (3.5) и полигармонического (3.6) воздействий. Однако такой метод определения спектра отклика оказывается весьма трудоемким. Поэтому на практике получили распространение специальные методы спектрального анализа, каждый из которых связан, как правило, с определенными способами аппроксимации нелинейной зависимости (3.3) и характером воздействующего сигнала.
Задача любого метода спектрального анализа заключается в таком преобразовании правой части (3.3), при котором отклик (ток) представляется в виде суммы гармонических слагаемых: амплитуды и частоты этих компонент определяют спектр отклика. Наибольшее распространение имеют методы, основанные на использовании: 1) тригонометрических формул кратного аргумента,
2) формул трех и пяти ординат, 3) функций Бесселя от мнимого аргумента, а также 4) угла отсечки.
МЕТОД, ОСНОВАННЫЙ НА ИСПОЛЬЗОВАНИИ ТРИГОНОМЕТРИЧЕСКИХ ФОРМУЛ КРАТНОГО АРГУМЕНТА
Этот метод является основным при использовании полиномиальной аппроксимации и особенно удобен для выявления принципа действия и основных особенностей таких устройств, как модуляторы, детекторы, преобразователи частоты, делители частоты и т. п.
Сначала рассмотрим воздействие на нелинейный резистивный элемент, характеристика которого аппроксимирована полиномом степени
гармонического колебания (3.4). Подставляя (3.4) в (3.7), получаем
Для представления правой части (3.8) в виде суммы синусоидальных компонент воспользуемся известными тригонометрическими
формулами, позволяющими заменить степени косинусов (или синусов) через тригонометрические функции кратных аргументов (отсюда название метода)
Осуществление такой подстановки и последующее суммирование коэффициентов при косинусах одинаковых аргументов позволяет записать (3.8) как
На рис. 3.6a построен спектр выходного сигнала (3.11) и отмечены амплитуды спектральных компонент.
Из сравнения выражений (3.11) и (3.12) с (3.4) следует:
1. Спектр отклика нелинейного элемента при воздействии на него гармонического сигнала оказывается линейчатым, содержащим ряд составляющих с частотами, кратными частоте входного сигнала. Наивысший номер составляющей спектра равен степени используемого поли «ом а. Поэтому, если для какого-то применения нелинейного элемента необходимо знать амплитуду гармоники отклика, вольт-амперная характеристика элемента должна быть аппроксимирована полиномом порядкане ниже
2. Постоянная составляющая отклика и амплитуды четных гармоник определяются только четными степенями напряжения в полиноме а нечетных гармоник — только нечетными.
3. Текущая фаза гармоники отклика с частотой раз больше значения текущей фазы (3.10) воздействующего сигнала:
Начальные фазы связаны соотношением
При воздействии бигармонического напряжения (3.5) на нелинейный элемент, аппроксимируемый полиномом (3.7),
Раскрываем скобки в правой части (3.15), используя в случае высоких степеней бином Ньютона, после чего с помощью тригонометрических формул представляем правую часть (3.15) в виде суммы гармонических составляющих различных частот. Для
Под каждым слагаемым записаны частоты, получающиеся при замене степеней и произведений косинусов суммой гармонических
составляющих на основании соотношений (3.9) и известного тригонометрического выражения
Из выражения (3.15) и частного случая (3.16) следует, что при воздействии бигармонического сигнала ток содержит три группы гармонических составляющих:
гармоники с частотами и начальными фазами где
комбинационные составляющие с частотами и начальными фазами где отличные от нуля целые числа любого знака.
Комбинационные частоты возникают в нелинейных цепях только в случае одновременного воздействия на них двух или большего числа гармонических колебаний. Комбинационные частоты принято характеризовать их порядком определяемым суммой коэффициентов: Простейшими являются комбинационные частоты второго порядка В случае в отклике содержатся комбинационные частоты второго и третьего порядков.
На рис. 3.66 построен спектр отклика (3.16) на воздействие бигармонического сигнала (3.5), причем комбинационные частоты выделены пунктирными линиями.
Если отношение частот не может быть представлено в виде отношения небольших целых чисел (случай асинхронных воздействий), то все гармоники и колебания комбинационных частот образуют различные частотные компоненты. В частности, первая гармоника тока частоты может быть записана как — е. она совпадает по фазе с воздействующим напряжением этой частоты.
Положение меняется, если отношение частот может быть выражено отношением небольшим целых чисел (случай синхронных воздействий)
где В этом случае ток может содержать несколько компонент одной и той же частоты с различными фазами. В качестве примера рассмотрим воздействие бигармонического колебания с
иа нелинейный элемент, описываемый полиномом второй степени
Подставляя (3.19) в (3.20), легко установить, что теперь первая гармоника тока частоты состоит из двух компонент:
из которых вторая является следствием возникновения комбинационной частоты второго порядка. Еслн, например, выражение (3.21) можно записать
Из выражений (3.22) и (3.23) следует, что в рассматриваемом случае:
имеет место сдвиг фаз между первой гармоникой тока частоты и воздействующим напряжением той же частоты; это означает, что резистивный нелинейный элемент (3.20) по отношению к воздействию частоты обладает комплексной средней крутизной или
величина сдвига фаз и амплитуды а значит, и величины активной и реактивной компонент средней крутизны зависят от амплитуды и фазы второго колебания (второй гармоники
Обогащение спектра отклика по сравнению со спектром воздействия происходит и в нелинейных реактивных цепях. Так, если на нелинейную дифференциальную емкость, аппроксимируемую относительно рабочей точки полиномом действует бигармоническое напряжение (3.5), в спектре тока
окажутся частоты, кратные и комбинационные частоты до третьего порядка включительно.
В п. 3.1 был изложен классический метод решения задачи спектрального анализа нелинейной цепи применительно к случаю гармонического воздействия с постоянным смещением на резистивный нелинейный элемент. Полученные результаты можно обобщить на случай, когда во входном воздействии есть не одна, а несколько гармонических составляющих. Тогда применяются кратные ряды Фурье. Если воздействие непериодическое, то вместо рядов Фурье надо использовать интегральную форму разложения Фурье.
Кроме громоздкого классического метода, широко применяются более простые специальные спектральные методы. Ряд методов основан на аппроксимации ВАХ изучаемого элемента. Аппроксимация упрощает спектральный анализ, но ухудшает точность получаемых результатов.
Кусочно-линейная аппроксимация. На ее применении основан метод угла отсечки. Форма тока в цепи, содержащей нелинейный элемент с характеристикой
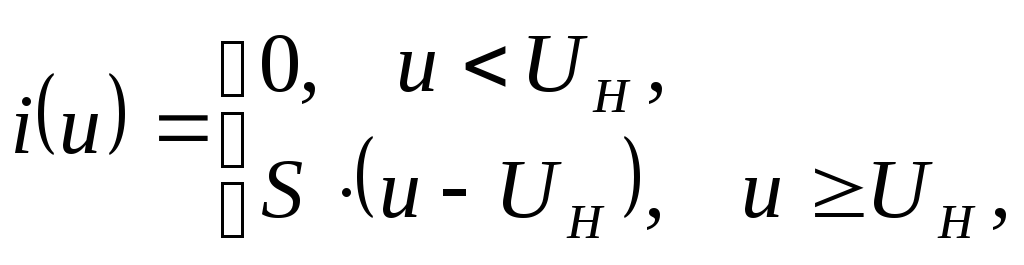
(3.5)
на который подано напряжение
, (3.6)
показана на рис. 3.2.
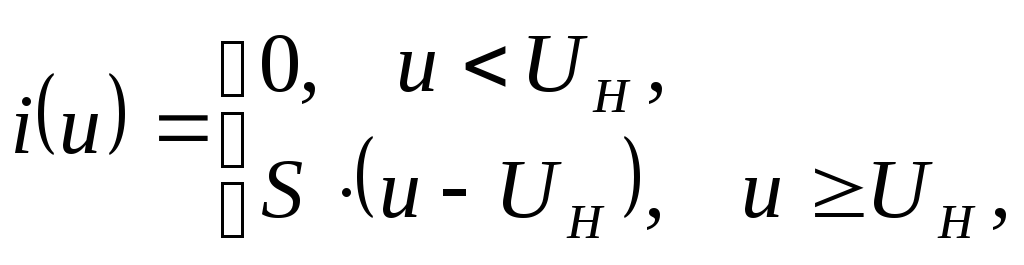
График тока имеет характерный вид периодической последовательности косинусоидальных импульсов с отсечкой. Искомая последовательность выражается аналитически при подстановке (3.6) в (3.5) как:
(3.7)
где , , , - параметр, называемый углом отсечки и определяемый из условия: как при ( равно половине части периода колебаний, когда протекает ток).
Спектр тока выражается формулой (3.3), где амплитуды компонент спектра находятся при подстановке (3.7) в выражения для этих коэффициентов, данные после (3.3):
(3.8)
где , - функция Берга ого порядка,

Для получения максимально возможного значения амплитуды с номером надо соответствующим образом выбирать .
Пример. Нелинейный элемент имеет кусочно-линейную ВАХ с параметрами В, мА/В. К данному элементу приложено напряжение , В. Вычислить постоянную составляющую и амплитуду первой гармоники тока .
Так как , то . Значения функций Берга:

По формулам (3.8) имеем мА, мА.

Степенная аппроксимация. На ее применении основан метод с использованием тригонометрических формул кратного аргумента. Пусть в окрестности рабочей точки вольт-амперная характеристика нелинейного элемента представлена в виде:
(3.9)
Приложенное к двухполюснику напряжение дается выражением (3.6). Используя известные формулы:

путем подстановки (3.6) в (3.9) получим выражение для спектра тока:

(3.10)

Из (3.10) следует общее выражение для амплитуды тока гармоники с номером :
(3.11)
Вывод: постоянная составляющая и амплитуды четных гармоник определяются коэффициентами степенного ряда с четными номерами. Амплитуды нечетных гармоник зависят лишь от нечетных коэффициентов.

Пример. Рассмотрим нелинейные искажения в транзисторном усилителе с резистивной нагрузкой , показанном на рис. 3.3.
Полагаем, что амплитуда входного гармонического сигнала достаточно велика, чтобы вызвать необходимость учета нелинейности проходной характеристики транзистора . Аппроксимируем характеристику в окрестности рабочей точки полиномом второй степени:
На вход усилителя подается напряжение
В коллекторной цепи получим спектр тока, содержащий постоянную составляющую, а также первую и вторую гармоники с амплитудами (см. (3.11)):
Читайте также:
